Definição do raio de curva e do ângulo de ataque através de três pontos

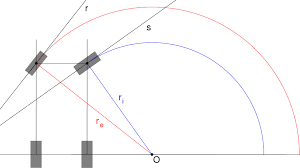
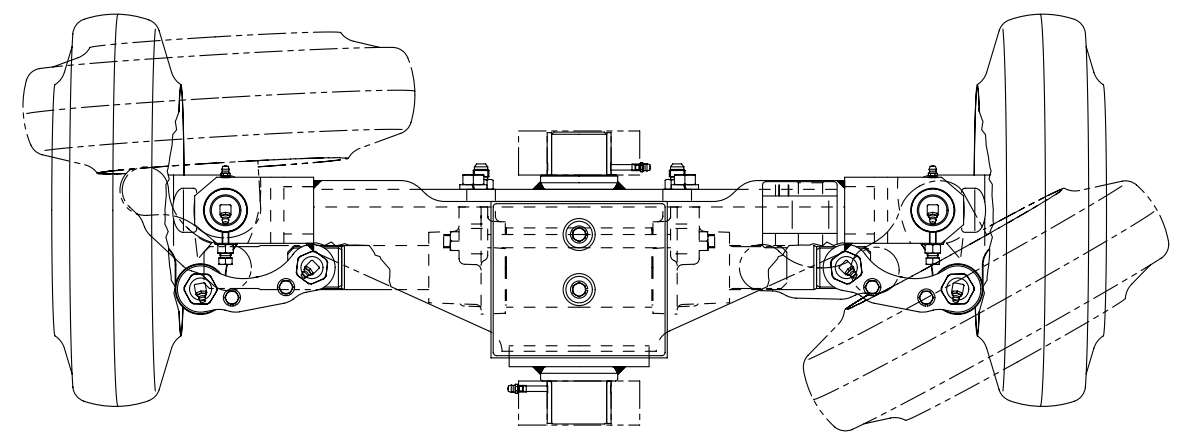
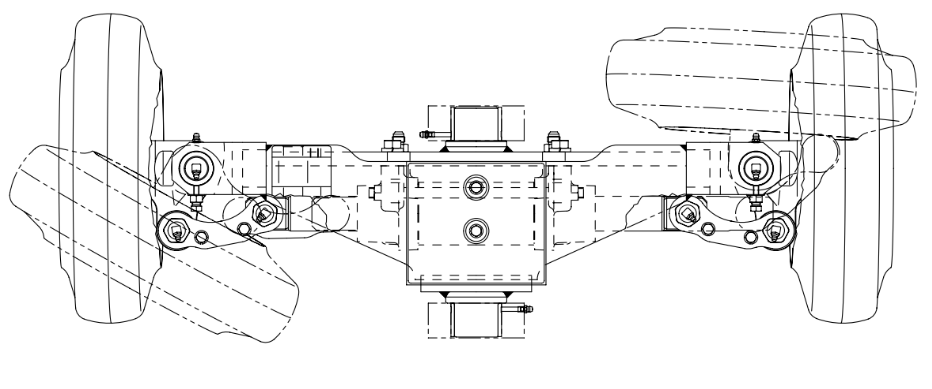
Ao obter os dados de medição do sensor da roda de uma empilhadeira elétrica  observamos que ela utiliza um sistema de direção pivotado excêntrico de forma a compensar a diferença angular nas duas rodas traseiras quando operando em curvas. Assim, o ângulo observado é diferente, de acordo com qual roda está no lado interno da curva. Corresponde efetivamente ao conceito da geometria de Ackerman.

Isso torna-se um problema na empilhadeira pois o sensor que monitora a posição do eixo não está montado no centro de um conjunto pinhão e cremalheira, e sim na ponta de um dos eixos. Curvas para um lado esterçam a roda quase totalmente na horizontal enquanto a outra roda oferece um ângulo ligeiramente inclinado. O inverso se observa quando a curva for feita para o lado oposto.

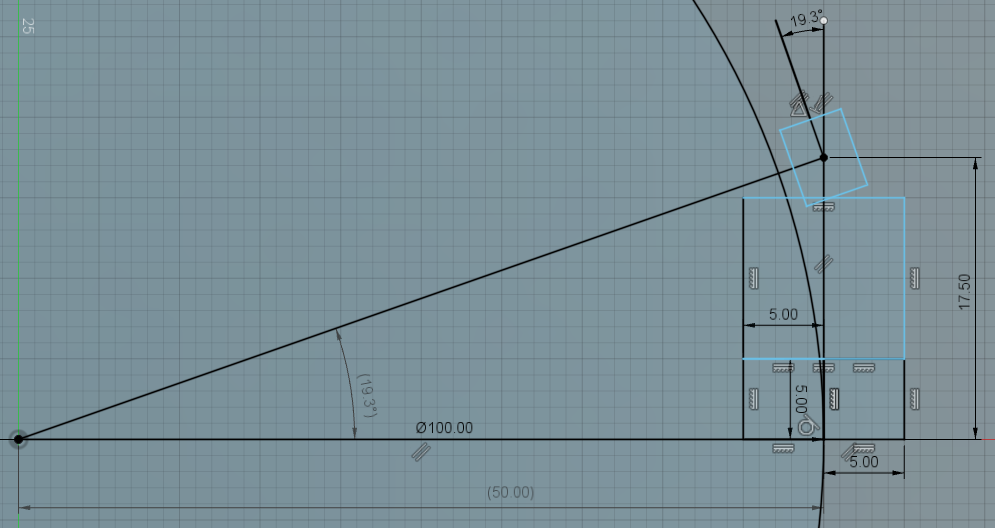
Através dos conceitos básicos de trigonometria e de semelhança de triângulos é possível determinar o raio da curva de um objeto em movimento circular (MC).

Para isso devemos utilizar as leituras dos scanners para definir o plano, ponto inicial, ponto intermediário e ponto final. Com três pontos não colineares é possível determinar uma circunferência única, relativa a um raio único.

O volante de direção deve ser acionado e registrado o valor lido de inclinação indicado pelo sensor.

Esse valor lido refere-se a inclinação na roda, que define o raio da curvatura.

Link da planilha

O objeto descrevendo a trajetória circular é sempre tangente ao ponto da circunferência e perpendicular ao raio. A distância entre eixos da empilhadeira forma o cateto oposto ao ângulo 𝞡, enquanto que o raio forma o cateto adjacente ao ângulo 𝞡. Por semelhança de triângulos ele é o ângulo de ataque da roda, ou de inclinação que acompanhará a circunferência.

Esse ângulo 𝞡 é o ângulo de inclinação da roda central ou equivalente à geometria Ackermann, como se fosse um triciclo. Ele é calculado pela função:

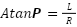
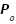: Theta Ackerman equivalente

L: Distância entre eixos

R: Raio do giro

O ângulo da roda interna à curva, que faz uma circunferência de raio menor, é calculado pela função:

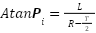
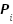: Theta interno

L: Distância entre eixos

R: Raio do giro

T: Distância entre rodas

O ângulo da roda externa a curva, que faz uma circunferência de raio maior, é calculado pela função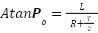

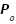: Theta externo

L: Distância entre eixos

R: Raio do giro

T: Distância entre rodas

 

Resultados esperados:

  • Criar tabela relacionando posição do sensor, ângulo Ackermann e raio obtido na curva
  • Passar ao MCU o valor final esperado do sensor de posição do steering para as posições relativas ao raio esperado.
  • Criar uma malha fechada que monitore e corrija a posição de steering em função do raio descrito pelos valores lidos nos scanners, corrigindo o deslocamento em tempo real.